Computer Graphics
CSE5280 Course Information
2D Transformations
A transformation is any operation on a point in space (x, y) that maps the point's coordinates into a
new set of coordinates (x1,y1).
References
- Computer Graphics Principles and Practice, Foley, van Dam, Feiner, and Hughes, Addison-Wesley ©
1997
- Computer Graphics, Schaum's Outlines, Plastock and Kalley, McGraw-Hill © 1986
- Principles of Interactive Computer Graphics, Newman and Sproull, McGraw-Hill ©1979
Translation
In translation an object is displaced a given distance and direction from its original position. If the displacement
is given by the vector v = txI + tyJ,
the new object point P'(x', y') can be found by applying the transformation Tv
to P(x, y). See the figure below
P' = Tv(P)
where x' = x + tx and y' = y +
ty.
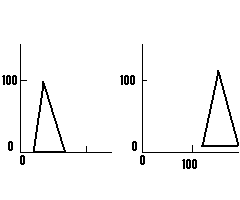
As an example, consider a triangle defined by three vertices (20,0), (60, 0), and (40, 100) being translated 100
units to the right along the x-axis ( tx = 100) and 10 units up along the y-axis
(ty = 10). The new vertices are (120, 10), (160, 10), and (140, 110), see figure
below:
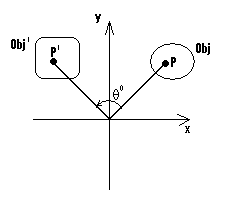
Rotation
In rotation, the object is rotated ø° about the origin. The convention is that the direction of the
rotation is CCW if ø is a positive angle and CW if the ø is a negative angle. The transformation
for rotation Rø is
P' = Rø(P)
where x' = x cos(ø) - y sin(ø) and y'
= x sin(ø) + y cos(ø)
For example a triangle (20,0), (60,0), (40,100) rotated 45° clockwise about the origin is (14.14, -14.14),
(42.43, -42.43), (98.99, -42.43)
Scaling
Scaling is the process of expanding or compressing the dimensions of an object. Positive scaling constants
Sx and Sy are used to describe changes in length with
respect to the x direction and y direction. A scaling constant > 1 creates an expansion (magnification)
of length, and < 1 a compression (reduction) of length. Scaling occurs along the x-axis and y-axis to create
a new point from the original. This is achieved using the following transformation:
P' = TSx,Sy
(P),
where x' = Sx * x ,and y' = Sy * y
If Sx and Sy are not equal, they have the effect of distorting pictures by elongating or shrinking
them along the directions parallel to the coordinate axes. The mirror image of an object can be generated by using
the negative values for Sx and Sy.
Homogeneous Coordinates
Translation, scaling and rotation were expressed non-homogenously:
P´ = P + T
P´ = S × P
P´ = R × P
Composition is difficult to express using the standard notation above. Homogeneous coordinates allow all three
to be expressed homogeneously, using multiplication by 3 × 3 matrices.
Add a third coordinate to a point P(x,y). So instead of representing the point using an (x,y) coordinate pair,
each point is represented by three values, (x, y, W).
P2d (x, y) -> Ph (wx, wy, w), w xb9 0
Given Ph (x, y, w), w xb9 0
Then P2d (x, y) = P2d (x/w, y/w)
W is 1 for affine transformations in graphics. Affine transformations have the property of preserving
parallism of lines, but not the lengths and angles. See example in figure 5.6 on page 207 in your Computer Graphics
text.
Shear an affine transformation
A shear is a transformation that distorts the shape of an object along either or both of the axies. Like scale
and translate, a shear can be done along just one or along both of the coordinate axes. A shear along one axis
(say, the x-axis) is performed in terms of the point's coordinate in the other axis (the y-axis). Thus a shear
of 1 in the x-axis will cause the x-coodinate of the point ot distort by 1*(y-coordinate).
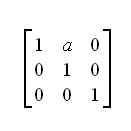
To shear in the x direction the equation is:
x1 = x + ay
y1 = y
Where b = 0
Where x1 and y1 are the new values, x and y are the original values, and a is the scaling factor in the x direction.
The matrix is as follows.
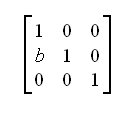
Shearing in the y direction is similar except the roles are reversed.
x1 = x
y1 = y + bx
Where a = 0.
Where x1 and y1 are the new values, x and y are the original values, and b is
the scaling factor in the y direction. The matrix is as follows.
Example
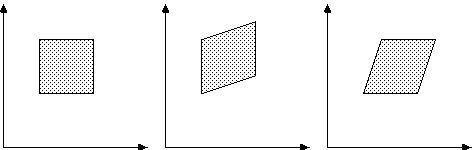
Original Y-Shear X-Shear
Reference Java 2D
Example
Composition
R(ø) rotates about the origin; to rotate about P1
- Translate P1 to origin
- Rotate
- Translate origin back to P1

Java Example(s)





